EEG/MEG Signal Processing for Successive Neural Network Control
The neural activity which is detected by electrodes on the helmet created by our experimental design team must undergo multiple stages of processing before being ready to be sent to our neural network. For our deep learning team to be able to optimally classify and execute further control based on these signals, it must have access to maximally clean, segmented waveforms describing exactly the neural activity it is meant to detect. This can be a difficult task given the notoriously low Signal-to-Noise Ratio (SNR) exhibited by EEG/MEG signals, however, given our multi-stage processing pipeline, it is possible to remove much of the different sources of noise corrupting our target signals. In this document, I will explain in-order the basic processing stages we implemented as of 05.2023 to achieve this task. The functions which are present within our processing files and are not mentioned in this document are experimental and require further testing. Therefore, they have not contributed to the results we have attained thus far. If you have any questions after reading this, feel free to contact me.
The first step in processing is to take a look at the raw data and identify which channels are suitable for use. During the experiment, there can be two types of recording malfunctions that can exist; either the electrode fails to acquire enough signal information or the electrode picks up far too much noise. In the first case, we tend to see a close-to-flatline signal while in the second case, we tend to see disproportionally large amplitudes rendering our SNR far too small. These two error types must be identified in the beginning stages of preprocessing, since we need accurate estimations of our noise for later noise-removal functions. Clearly these malfunctioning channels offer a noise component to the total average which is either far too large or too small, along with potentially having different statistical properties in comparison to the other channels. Thus, it is important to identify these channels to stop them from influencing any further computations.
MNE offers an object called ‘info’ which, among other things, maintains a list of channel indices corresponding to channels unsuitable for use. Since some channels may be properly functioning during one timespan during an experiment, then malfunctioning during another, this "bad channel rejection list" allows us dynamically update the list of bad channel indices so that we need not delete potentially useful data from our processing procedures. This list is a part of the ‘Raw’ object (i.e. the raw experimental data) and is automatically propagated through any later stages of processing.
After identifying any unsuitable channels, it is important to decide whether these channels should be added to this rejection list, or whether they should be instead interpolated using the signals coming from neighboring channels. In cases where the number of electrodes is very small along with the amount of available data, it is preferrable to interpolate the bad signal rather than to ignore it. This is due to the analogous fact that deleting an independent row from a rank-5 matrix removes more information content than removing it from a rank-500 matrix. This interpolation can easily be done using MNE's ‘interpolate_bads()’ method.
If maintaining the same dimensionality of the data is not as important as removing abnormal noise, then the ‘raw.info["bads"]’ list should be updated based off of the two aforementioned rejection criteria, namely minimum (flatline) and maximum amplitude peak-to-peak ratios.
Once the unsuitable channels have been identified and dealt with, the next step is to identify the reference potential for our EEG data (if none is provided by our raw data). Since EEG signals measure voltage changes over time, a ground potential must exist. In the recording process, usually a specific electrode is designated to be the reference node and is placed in a position where ideally none of the brain functions are measured and all of the noise sources are. If there was no pre-defined reference electrode during the experiment, then the recording software either chose an arbitrary electrode or used the average signal yielded by some subset of electrodes. A commonly recommended approach in case of no pre-defined reference electrode, is to use the average of all electrode signals. This is due to the small model error that exists at each channel. If we were to choose any specific electrode (or subset of electrodes) then we would be biasing the error in the direction of the chosen electrodes. Thus it is generally recommended to give an even weighting to all electrodes under a total average. MNE offers the ‘add_reference_channels()’ and ‘set_eeg_reference()’ functions to specify the desired reference, along with the possibility to average any group of electrode signals and use this average as the reference potential.
Now the channels are ready for application-specific preprocessing. Most experiments will have some channels within the raw data set corresponding to the onset of different stimuli over the duration of the experiment. We are interested in the subject's response to these different stimuli, so these "STIM" channels allow us to know which time-segments of the raw data we need to analyze. MNE offers a ‘find_events()’ function which takes both the raw data and the channel indices corresponding to the STIM channels as an input, and outputs an events array. This array tells us at which sample point which stimuli was administered, and maps each unique event to a number defining the event-ID. This events array conveniences the user in further categorizing and organizing the raw data. MNE offers functions which can extract and pool together raw signals corresponding to different events through this events array, as well as fine-tuning features to move the sample number along the onset/offset of each stimulus.
The events array is essentially a mapping between signal sample number and event-ID, so when presenting the data to other people who are not familiar with the python program, these numbers will not be immediately clear. MNE offers a user-friendly way to present the events on top of the raw data, and this is through annotations. The ‘Annotations’ object takes as an input the onsets of all stimuli (which can be found by use of the events array), the user-defined duration of each stimuli along with a list of strings offering the desired annotations for each event. In the case than a dictionary has been defined mapping each sample number to an event-ID, then the ‘annotations_from_events()’ function can quickly map each event to an annotation (or ‘events_from_annotations()’ if you would like to retrieve the event-ID's from some set of annotations). If there are some specific events/annotations that must not be used in further processes, then the ‘reject_by_annotation’ parameter in MNE functions allow us to ignore components based off of these annotations. Often there are breaks between experiments or change of stimuli, and in such cases it can be useful to annotate these breaks in the experiments. For this, the ‘annotate_break()’ function automatically will read through the data set, find, and annotate these breaks. Its parameters allow for more control over this procedure, but its default parameters often do this sufficiently well.
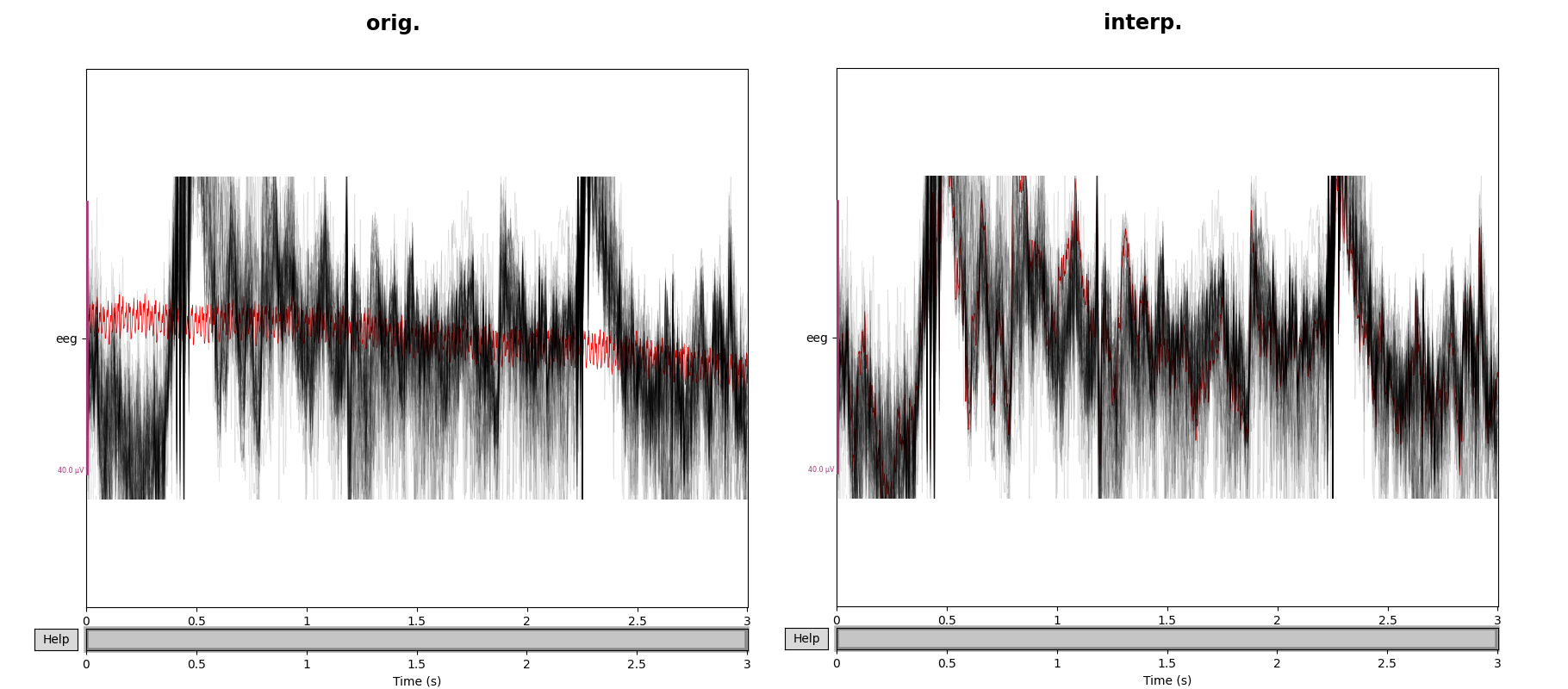
After identifying and annotating the data suitable for further processing, the next step is to isolate, segment and categorize the signals. We are interested in extracting the cleanest signal corresponding to the user's reaction to some stimulus. The short timespan which corresponds to this reaction in called an epoch. The raw data and the events array are the minimum data required to create epochs. We can construct the object by calling the following example function,
epochs = mne.Epochs(raw, events, tmin=-0.3, tmax=0.7, event_id=event_dict, preload=True)
epochs.plot(n_epochs=10, events=True)Which can then be visualized by calling the above plotting function.
We can see from the above image that the individual epochs are sequentially numbered, and separated by the black vertical lines. Within the Epoch constructor, you can specify the time relative to each event at which to start and end the timespan of the epoch. Within this constructor, is important to set the ‘baseline’ parameter to ‘None’ if the noise removal processes come after epoching. This is because baseline correction1 introduces errors into the ICA noise removal processes. After creating the epochs, we now have isolated signals corresponding to the onset of each stimulus administered during the experiment. These epochs can be pooled together thanks to the eventID's/annotations associated with each epoch.
The ICA algorithm is designed to estimate components of non-gaussian and independently generated sources which are superpositioned with unknown amplitude coefficients. MNE implements 3 different ICA algorithms. Two of them (FastICA and Infomax) are already widespread in use, and the third (Picard, the newest one) tends to converge faster in cases where the sources are not completely independent. Before ICA is applied, there is a principal component decomposition which is applied to the data. ICA then reassembles these principal components into an equal number of components, which are estimates of the original signals stemming from their independent sources. The way ICA works in MNE, is that first an ICA object is created, e.g.
ica = ICA(n_components=30)
And then this object is fitted and then applied to the prefiltered, raw data, e.g.
ica.fit(raw_data_filtered)
ica.exclude=[‘Desired ICA Indices’]
ica.apply(raw_data_filtered or raw)
In creating the ICA object, you specify upon how many signals you want to fit the ICA algorithm with the parameter ‘n_components.’ The ICA algorithm automatically applies principal component analysis (PCA) onto all the channel signals, and then it selects the first ‘n_components’ PCA signals to then send into the actual ICA procedure. The reason for automatically doing first PCA and then ICA, is that PCA will organize the channel matrix (containing all the channel-specific signal samples over time) into another matrix organized top-down from strongest to weakest as a result of the eigenvalue/vector decomposition. This way, the ICA procedure has sorted access to the signals which influence all the individual channels the most. The idea is then, to reassemble them into an equal number of signals which correspond to (what is most likely) the signals stemming from independent sources.
After the ICA object is created with a certain specified number of components, we now must apply this object onto the data using ‘ica.fit()’. After this is done, the actual ICA procedure has been executed, and we now have e.g. 30 signals estimated to be the outputs of whatever independent sources are present during the experiment. The next step is to investigate these 30 components and decide which signals we want to nullify. This can be done either visually by the programmer, or through an automatic MNE function which is designed to find common artifacts such as heartbeat, muscle-postural or ocular influences.
When using the MNE functions to find one of these three common artifacts, we must be careful as the procedure for how to handle these artifacts differs due to our BCI not having ECG/EOG specific electrodes. Heartbeat and muscle artifacts are the easiest for us to deal with. The MNE function ‘find_bads_ecg()’ is designed to identify heartbeat signals from our independent components. In cases (such as ours) where we do not have a heartbeat-specific electrode, this function cross-averages the magnetometer/gradiometer channels to construct a virtual ECG channel. Applying this function onto the data, returns both the indices corresponding to the IC’s which match the ECG-specific pattern, as well as a list of scores which tell us with which confidence each IC matches the ECG pattern. After finding these indices, we then add these indices to the list of IC’s to exclude.
We can see the above plotted returned signals post-fitting by the ICA algorithm. The first ICA component looks like a typical ocular artifact, while the second ICA component looks like a typical heartbeat artifact. Both of these components would by found automatically by the MNE functions designed to identify them. The same procedure is done for muscle artifacts, where instead we use the ‘find_bads_muscle()’ function.
Muscle artifacts are much more pronounced in EEG channels than MEG, so since we do a simultaneous recording, it is recommended to execute ICA on EEG and MEG separately. We consider only EEG channels by,
raw.pick_types(eeg=True)
Muscle IC’s also exhibit patterns which we can use to visually identify them. Specifically, when plotting the power spectrum, they attain a minimum around 10 Hz and a maximum around 25 Hz, which in a loglog scale, generally results in a visibly positive slope between 7 and 75 Hz. Another way to identify these artifacts is through their single focal point in the topomap, which appears in stark contrast to neural activity which is much more spread out across the topomap.
The last missing artifact to remove are now EOG artifacts, which come with an important caveat. Unlike in ECG and muscle artifacts, ‘find_bads_eog()’ is not able to reliably cross-average the different channels to construct a virtual channel, which ICA can then accurately use as a pattern to compare all ICs with. For these ocular artifacts, it is necessary to designate a proxy channel or two (using ‘ch_name’) which serve this purpose.
find_bads_eog(raw, ch_name=insert_here)
The caveat to keep in mind is that the more the designated channels capture relevant prefrontal cortex neural activity, the higher the performance degradation.
Reference: All images were taken from the MNE library website.